여러분들은 어디 사시나요? 저는 현재 대한민국 서울에 살고 있습니다. 하지만 제가 저의 위치를 설명하는 방식은 지구라는 행성 위에서 대한민국이라는 나라 안에 서울이라는 도시를 여러분이 알고 있기 때문에 적절한 설명이 되죠. 그렇다면 만약 아무런 물체도 없는 공허한 곳에서 무엇을 '기준' 삼아 저의 위치를 설명할 수 있을까요?

우리는 저번 시간에 자연을 설명하는 두 가지 도구, 벡터와 스칼라에 대해서 알아보았는데요. 이 중에서 벡터라는 아이를 이용하여 위치를 설명하는 방식이 있습니다. 바로 '위치벡터'입니다!
위치벡터 개념을 설명하기 위해서 벡터를 '좌표공간'이라는 곳에 놓아봅시다. 좌표공간은 우리가 흔히 생각하는 x축, y축, z 축으로 이루어진 무한한 3차원 공간입니다. 그 공간에 있는 어떤 점을 (x, y, z)로 나타낼 수 있죠. 여기서 'r 벡터'라는 벡터의 시점을 좌표공간의 원점, 즉 (0,0,0)에 두고 종점을 좌표 공간의 어떤 점을 가리키도록 한다면
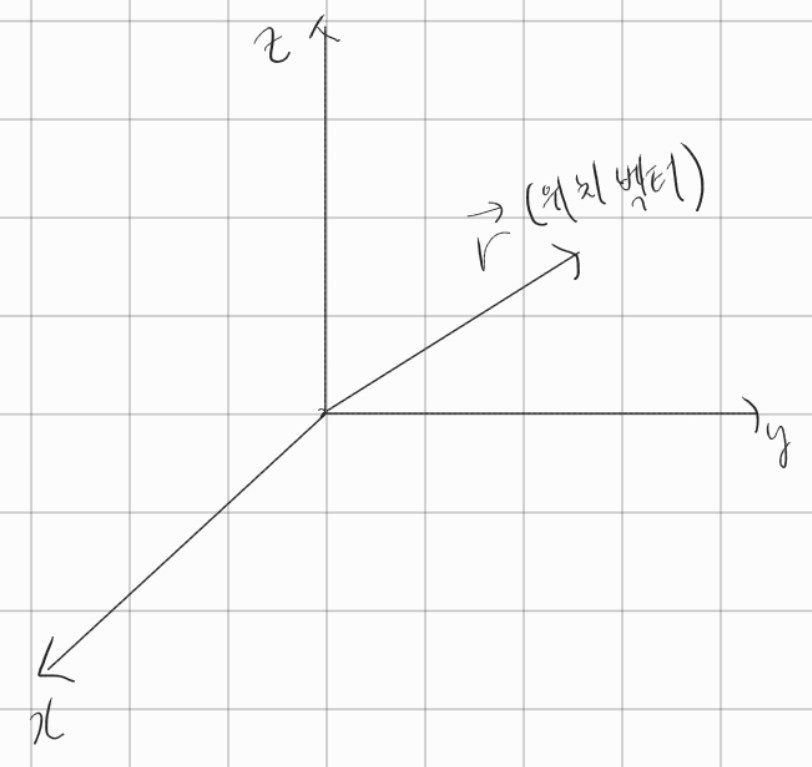
이런 모양이 됩니다. 그리고 이 'r 벡터'를 위치벡터 (position vector)라고 부릅니다. 이제 이 벡터는 공간상의 한 점의 위치를 나타내는 벡터입니다. 원점에서부터 떨어진 거리를 '크기'로 가지고 특정 '방향'을 가지고 있으니 벡터라고 할 수 있죠.
그리고 또 하나, 이전 글에서 설명했다시피 벡터는 다른 벡터들로 분해가 가능하죠. 그래서 'r 벡터'를 x축 방향, y축 방향, z 축 방향벡터, 총 3개의 벡터의 합으로 나타낼 수 있습니다.

그리고 3개의 벡터를 각각 x성분, y성분, z성분이라고 하겠습니다.
혹시 이전에 설명했던 "rank 1 tensor" 이미지의 3개의 수가 각각 x좌표, y좌표, z좌표를 담당한다면 조금 이해가 되실까요? 아직 어색하실 수 있고 지금은 잊어도 됩니다.
벡터의 방향이 저 화살표가 가르키는 방향이라면 벡터의 크기는 저 화살표의 길이를 구하는 방식으로 이루어집니다. 피타고라스의 원리를 사용하면 각 성분을 제곱해서 더한 값의 제곱근을 구하면 됩니다.
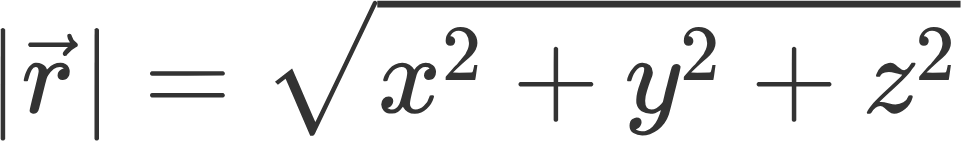
자, 이제 '기저벡터'라는 것에 대해서 알아봅시다. 일단 먼저 3차원 좌표공간에서의 기저벡터에 대해서 설명해보겠습니다.
아까 위치벡터를 3개의 성분으로 분해했는데요. 이제 이 성분벡터들을 크기가 "1"이고 방향은 '축' 방향인 '단위벡터'의 상수배로 바라볼 수도 있죠. 예를 들어서 원점과 (2,1,3)을 연결하는 위치벡터는 "2*(x축 방향으로의 단위벡터) + 1* (y축 방향으로의 단위벡터) + 3* (z축 방향으로의 단위벡터) " 가 되는 것입니다.

이렇게 나타낼 수 있습니다. 그리고 '기저벡터'는 이러한 '단위벡터'의 일반형입니다. 우리가 느끼는 세상은 3차원이지만 물리, 수학에서는 0차원부터 n차원까지 다양한 공간을 상상할 수 있습니다. 실재하는지는 모르지만 '논리적'으로는 가능한 공간이죠. 그래도 당분간은 3차원 공간 안에서만 이야기를 전개할 생각이니 너무 걱정하지 마세요...

이렇게 2가지 형태로 나타낼 수 있습니다. 기저벡터는 2가지 조건을 만족해야 합니다. 바로 크기가 '1'이고 서로 '수직'이어야 한다는 조건이죠. 기저벡터는 단위벡터의 일반형이니 크기가 '1'인 건 알겠는데, 서로 '수직'이라는 건 3차원을 넘어서는 영역에선 무슨 의미일까요? 이는 벡터의 연산에 대해 더 공부해보며 알아보도록 하겠습니다.
자 여기까지 위치벡터와 기저벡터에 대해서 알아보았습니다. 너무 어려우신가요...? 그래도 조금만 익숙해지면 충분히 이해할 수 있을겁니다. 그럼 좋은 하루 보내세요!
'물리를 위한 기초수학' 카테고리의 다른 글
| 정보를 숫자에 담다: 행렬의 종류 (1) | 2024.01.15 |
|---|---|
| 정보를 숫자에 담다: 행렬(matrix) (1) | 2024.01.13 |
| 벡터 심화 연산 (0) | 2024.01.07 |
| 벡터의 연산: 내적과 외적 (1) | 2024.01.05 |
| 자연이 선택한 두 가지 논리 도구: 벡터와 스칼라 (0) | 2023.12.27 |



