우리는 앞선 글에서 벡터의 정의와 간단한 성질에 대해서 알아보았습니다. 오늘은 벡터의 새로운 연산인 내적과 외적에 대해서 알아보도록 합시다!
먼저 내적에 대해 살펴보겠습니다. 영어로는 'dot product' 또는 'scalar product'라고 부르기도 합니다.
두 벡터가


이렇게 정의 됐을 때, 내적의 정의는 다음과 같습니다.

이 정의는 반드시 기억을 해주시기 바랍니다.
내적의 연산 결과는 어떤 값, 즉 '스칼라'로 나옵니다. 그리고 이 값은

와 같기도 하죠. 이때 Ө는 두 벡터 사이의 각도입니다. 그렇다면 왜 이 둘이 같을까요?
일단 어떤 벡터 x가 있을 때,

입니다. (1) 식은 내적의 정의와 벡터의 크기를 구하는 방법을 아신다면 납득할 수 있을 겁니다. 그렇다면 두 벡터 a, b가

이렇게 있을 때, 코사인법칙을 사용하면

임을 알 수 있는데 여기서 (1)식의 'x'에 'b벡터 - a벡터'를 대입하면
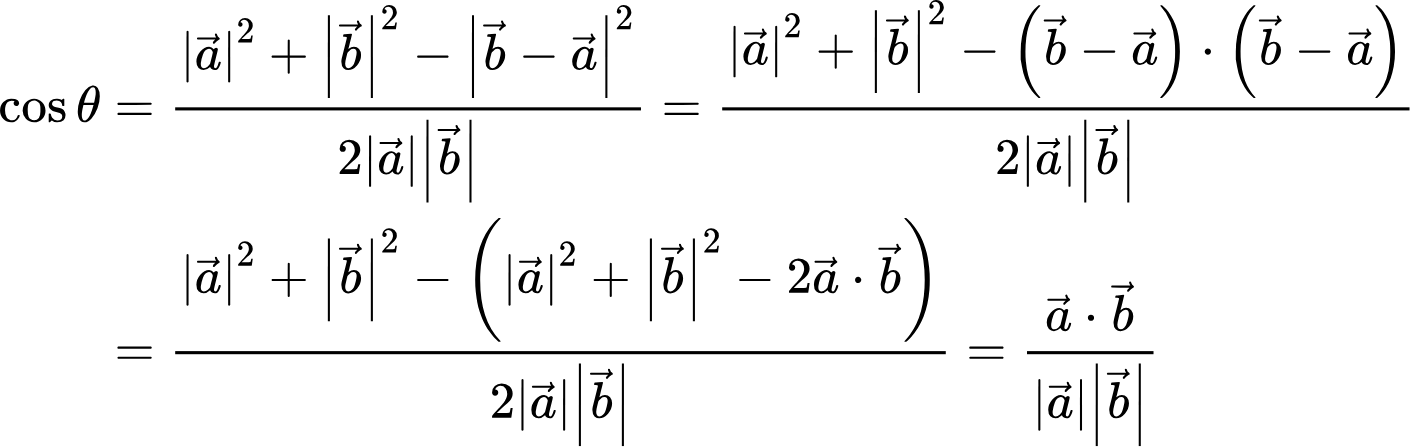
가 성립합니다.
그래서 만약 두 벡터가 서로 수직이다? 그렇다면 두 백터를 내적한 값은 0입니다. 이 성질을 잘 기억해 주시기 바랍니다.
다음으로 외적에 대해서 알아보도록 하겠습니다. 외적은 영어로 'cross product' 또는 'vector product'라고 합니다.
일단 외적은 3차원에 국한에서 보도록 하겠습니다.
외적의 정의는 다음과 같습니다.

일단 내적보다는 많이 복잡한 것 같습니다. 하지만 이 정의는 일단 있는 그대로 받아들여주시기 바랍니다. 외적이 내적과 다른 점 하나는 연산의 결과가 '벡터'로 나온다는 것입니다. 보시다시피 '기저벡터'를 뜻하는 기호가 있죠.
그리고 이 식의 ' εijk'는 다소 생소할 수 있습니다. 이 기호는 'levi civita'라고 불리는 기호로 다음과 같은 성질을 가지고 있습니다.
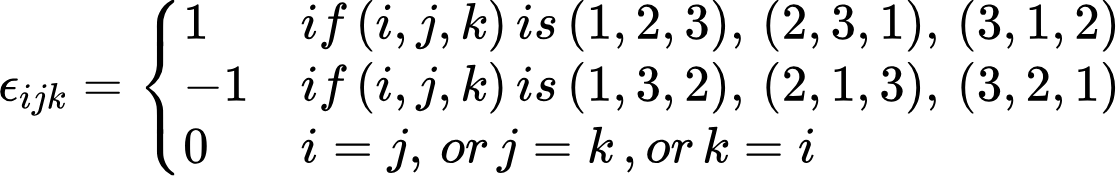
쉽게 말해서,

이 법칙을 만족합니다. 사실 levi civita는 3차원 이상에서도 비슷하게 정의가 되지만 일단 3차원만 다루도록 하겠습니다.
그래서 외적의 정의를 전개하면,

가 됩니다. 그리고 이 '벡터'의 크기는

와 같고(Ө는 두 벡터 사이의 각도) 방향은 '두 벡터 모두와 수직인 방향'입니다. 이 성질을 반드시 기억해 주시기 바랍니다.

(2)의 증명은 다음과 같습니다. 대충 넘겨봐도 무방합니다....

자, 여기까지 내적과 외적에 대해서 알아봤습니다. 이 두 연산은 물리를 배우면서 정말 끊~~임~~없~~이 등장하는 연산이니 이번 기회에 잘 알아두셨으면 좋겠습니다. 그럼 오늘도 좋은 하루 보내세요!
'물리를 위한 기초수학' 카테고리의 다른 글
| 정보를 숫자에 담다: 행렬의 종류 (1) | 2024.01.15 |
|---|---|
| 정보를 숫자에 담다: 행렬(matrix) (1) | 2024.01.13 |
| 벡터 심화 연산 (0) | 2024.01.07 |
| 자연이 선택한 주소: 위치벡터와 기저벡터 (2) | 2023.12.28 |
| 자연이 선택한 두 가지 논리 도구: 벡터와 스칼라 (0) | 2023.12.27 |



