안녕하세요! 저번 글에 이어서 오늘은 행렬식에 대해서 알아보도록 하겠습니다.
행렬식은 정방행렬에서 구하는 하나의 값입니다. 행렬 A가 있다면, A의 행렬식은

이렇게 2가지 방법으로 나타낼 수 있습니다. 만약 A가 2x2 행렬이라면,

이렇게 구합니다. 기하학적인 의미는

(a,b), (c,d)를 위치벡터로 봤을 때 두 벡터가 만드는 평행사변형의 넓이와 같습니다. 그렇다면 여기서, 외적이 생각나지 않나요? 외적한 값의 크기는 바로 두 벡터의 크기를 곱한다음 두 벡터의 사잇각의 사인값을 곱하는 것이었습니다.

(a,b)를 x벡터, (c,d)를 y벡터로 본다면 충분히 상상해볼 수 있습니다. 이와 같이 외적과 행렬식은 매우 밀접한 연관이 있습니다.
이제, 3x3 행렬의 행렬식을 봅시다.

이 식의 2x2 행렬식을 풀어서 쓰면 우리가 봤던 3차원 벡터의 외적 식과 똑같지 않나요...?

그럼 이 행렬식은 어떻게 구해진 것이냐!
먼저, 행렬에서 하나의 행이나 열을 정합니다. 이때, 최대한 0이 많은 행이나 열을 구하는 것이 좋습니다.
행이나 열을 하나 정했다면, 그 중에서 하나의 요소를 정합니다. 그 요소가 i행, j열에 있다면, i행과 j열을 제외한 나머지 숫자들로 그대로 행렬식을 다시 만듭니다. 새로 만든 행렬식의 계수는 ((-1)의 i+j제곱승)x(i행 j열의 수)로 정합니다. 이를 시각화하면

이렇게 됩니다. 그리고 이 작업을 처음에 정한 행이나 열의 나머지 수에 대해서도 반복합니다. 어렵지 않죠? 외적이 뭔지 안다면 금방 할 수 있을 것입니다. 저는 처음에 1행을 잡고 계산을 했는데요, 2열을 잡고도 계산할 수 있습니다.
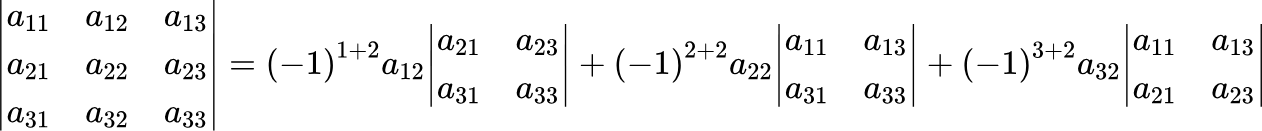
결국엔 같은 결과가 도출됩니다.
이렇게 행렬식을 구하는 방법을 '여인수 전개' 라고 합니다. i행과 j열을 제외한 나머지 숫자들로 만든 행렬식을 '소행렬식(minor)'라고 하고 소행렬식과 앞의 계수를 곱한 것을 '여인수'라고 합니다. 여인수를 기호로 나타내면

이렇게 나타낼 수 있습니다.
제가 직접 시범을 보인 행렬식은 3x3까지지만 nXn으로 무한히 확장할 수 있습니다. 그렇다면 이 작업을 엄청나게 많이 반복해야겠죠. 이 작업을 조금 더 간단히 하기 위해서 '기본 행 연산'이라는 규칙을 알아야 합니다. 이에 관해서는 다음에 다루도록 하겠습니다.
그럼 모두 좋은 하루 보내세요!
'물리를 위한 기초수학' 카테고리의 다른 글
| 정보를 숫자에 담다: 행렬식의 성질 (0) | 2024.01.18 |
|---|---|
| 정보를 숫자에 담다: 행렬의 연산 (2) | 2024.01.16 |
| 정보를 숫자에 담다: 행렬의 종류 (1) | 2024.01.15 |
| 정보를 숫자에 담다: 행렬(matrix) (1) | 2024.01.13 |
| 벡터 심화 연산 (0) | 2024.01.07 |



