저번 글에 이어서 오늘은 행렬의 종류에 대해서 알아보도록 하겠습니다!
1. 일반적인 행렬(matrix)

그냥 일반적인 행렬 그 자체입니다.
2. 정방행렬(square matrix)

정방행렬은 행과 렬의 개수가 같은 정사각형 모양의 행렬입니다.
3. 대각행렬(diagonal matrix)

대각행렬은 정방행렬 중에서 주 대각선의 요소 외의 다른 요소가 0인 행렬입니다.
4. 상삼각행렬(upper triangular matrix)

주 대각선 기준 아래에 있는 요소들이 모두 0인 정방행렬입니다.
5. 하삼각행렬

주 대각선 기준 위에 있는 요소들이 모두 0인 정방행렬입니다.
6. 전치행렬(transposed matrix)

전치행렬은 원래 행렬의 행과 열을 뒤바꾼 행렬입니다. 2행 3열에 있던 수는 3행 2열에 가고 3행 1열에 있던 수는 1행 3열로 서로 위치를 바꾼 행렬입니다. 기호는 T를 원래 행렬의 오른쪽 위에다 쓰면 됩니다.

그리고 전치행렬의 요소를 기호로 나타내면, 각 요소의 행과 열을 뒤바꾼 것이므로

이렇게 바꿀 수 있습니다.
7. 단위행렬(identity matrix)
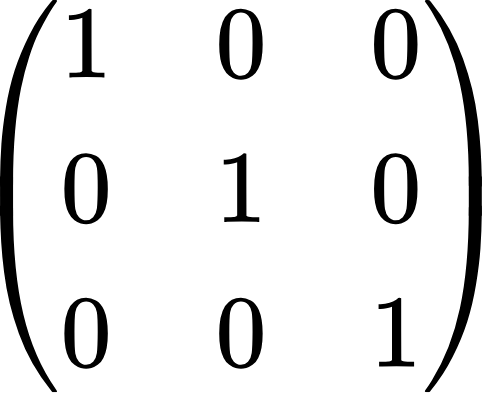
대각행렬 중 주 대각선의 요소가 모두 1인 행렬입니다. A라는 행렬에 단위행렬을 곱하면 다시 A행렬이 나옵니다. 행렬에 곱셈에 대해서는 다음 글에서 다루도록 하겠습니다. 기호로 I라고 나타냅니다.

8. 0행렬(zero matrix)

행렬의 모든 요소가 0인 행렬입니다. 꼭 정방행렬일 필요는 없습니다.
9. 역행렬(inverse matrix)

어떤 행렬에 그 행렬의 역행렬을 곱하면 단위행렬이 나옵니다. 행렬의 곱셈에 대해서는 다음 글에서 다루도록 하겠습니다.
여기까지 행렬의 종류를 대략적으로 알아봤습니다. 다음에는 행렬의 연산에 대해서 알아보도록 합시다!
그럼 좋은 하루 보내세요!
'물리를 위한 기초수학' 카테고리의 다른 글
| 정보를 숫자에 담다: 행렬식(determinant) (0) | 2024.01.16 |
|---|---|
| 정보를 숫자에 담다: 행렬의 연산 (2) | 2024.01.16 |
| 정보를 숫자에 담다: 행렬(matrix) (1) | 2024.01.13 |
| 벡터 심화 연산 (0) | 2024.01.07 |
| 벡터의 연산: 내적과 외적 (1) | 2024.01.05 |



