'인생은 속도가 아닌 방향'이라는 말 누구나 한 번쯤 들어보셨을 겁니다. 저는 이 말이 마음에 굉장히 와닿습니다. 특히나 요즘 SNS에서 '영 앤 리치' 행세가 유행을 타면서 누구나 빠르게 돈을 벌고 싶어 하고 일확천금의 기회를 노리는 사람들도 많아진 것 같습니다. 그래서 이때 우리가 다시 한번 '인생은 속도가 아닌 방향'이라는 말을 되새겨봐야 하지 않을까요...?
하지만 물리학의 관점에서는 이 말은 틀린 말입니다.... 왜일까요?
그전에 '벡터'와 '위치벡터'에 대해 모르시는 분들은 아래 링크를 한번 보고 와주세요!
https://wgco-physicspark.tistory.com/4('벡터와 스칼라' 편)
https://wgco-physicspark.tistory.com/5('위치벡터와 기저벡터' 편)

이유를 알기 전에 우리는 속도의 개념을 명확히 알아야 합니다. 그리고 속도에 대해서 배우기 전에 '변위'에 대해 먼저 알아봅시다.
변위란 '위치의 변화량'입니다. 정말 간단하죠?
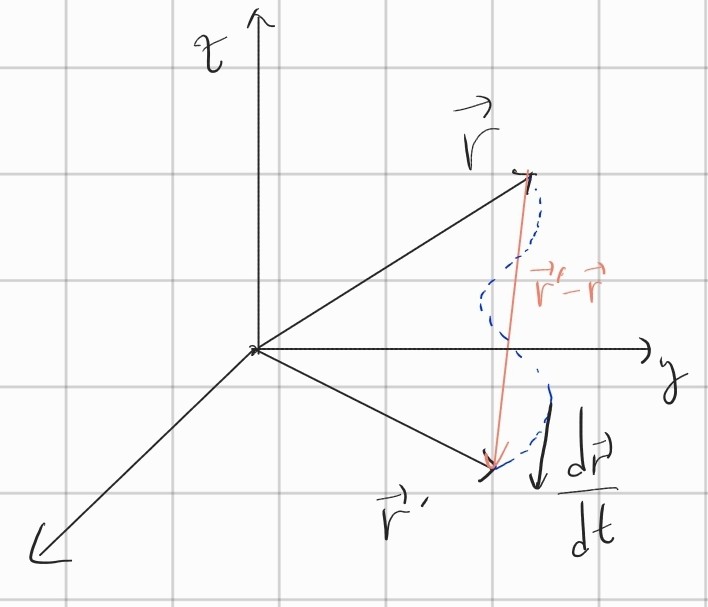
어떤 물체가 좌표공간을 돌아다닌다고 해봅시다. 만약 처음 위치를 'r벡터'라고 하고 일정 시간 후에 도착한 위치를 'r프라임 벡터'라고 한다면 변위는 나중 위치벡터에서 처음 위치벡터를 뺀 벡터가 되는 것이죠. 그림으로 표현하면
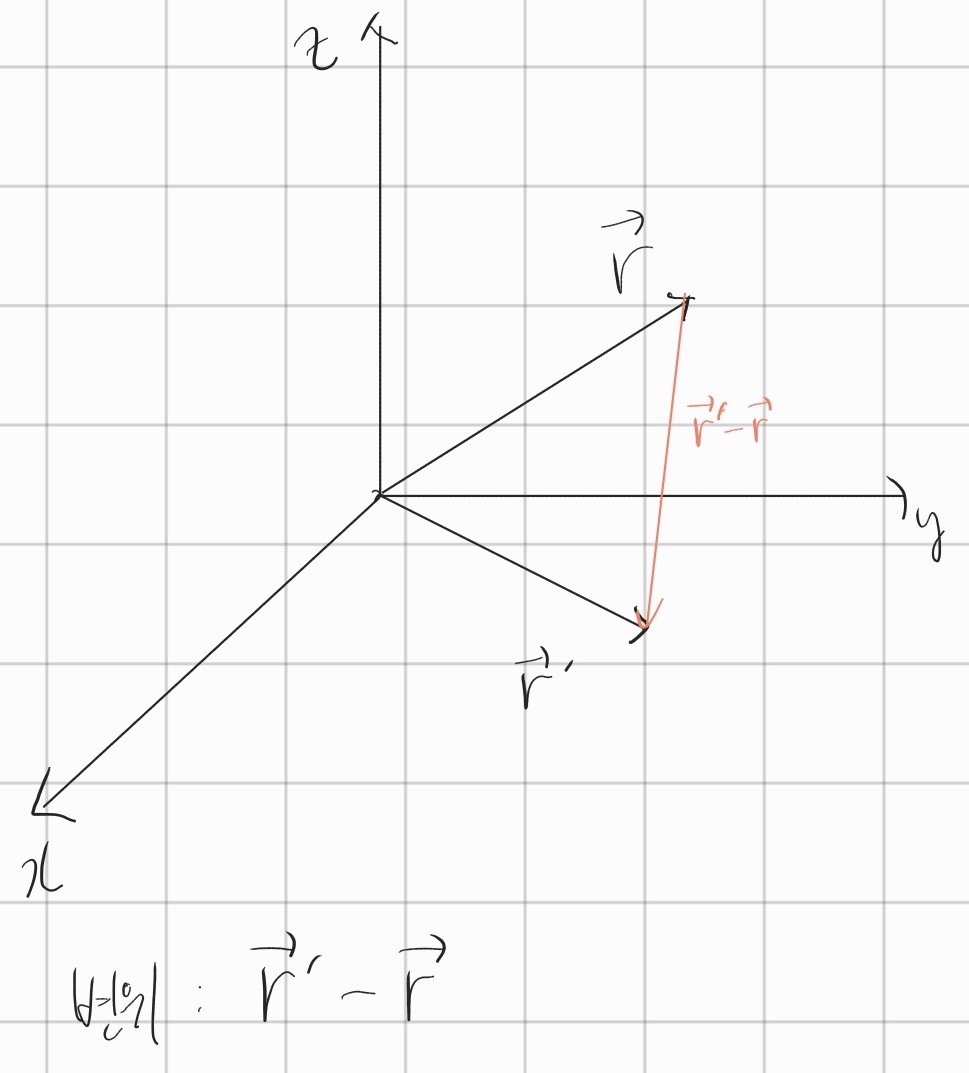
이렇게 됩니다. 보시다시피 변위는 크기와 방향을 가진 벡터입니다. 그리고 이동거리는 이 변위의 절댓값이죠. 그래서 변위와 이동거리를 헷갈릴 수 있지만 엄연히 다른 개념입니다.
이제 우리는 물체가 얼마나 이동했는지는 알았으니 다음으로 얼마나 빠르게 물체가 이동했는지를 알고 싶은 것입니다. 이를 위해서 '변위'를 '이동시간'으로 나누는 것이죠.
변위를

로 정의하고, 이동시간을

로 정의한다면 물체가 일정 시간 동안 움직인 '평균 속도'는
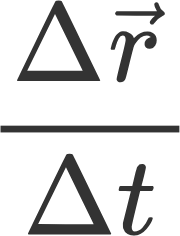
가 될 것입니다. 하지만 이것은 말 그대로 평균적인 속도입니다. 만약 이 시간 동안 물체의 이동경로가 구불구불하다면 물체의 순간, 순간마다의 속도는 평균속도와 다를 것입니다.
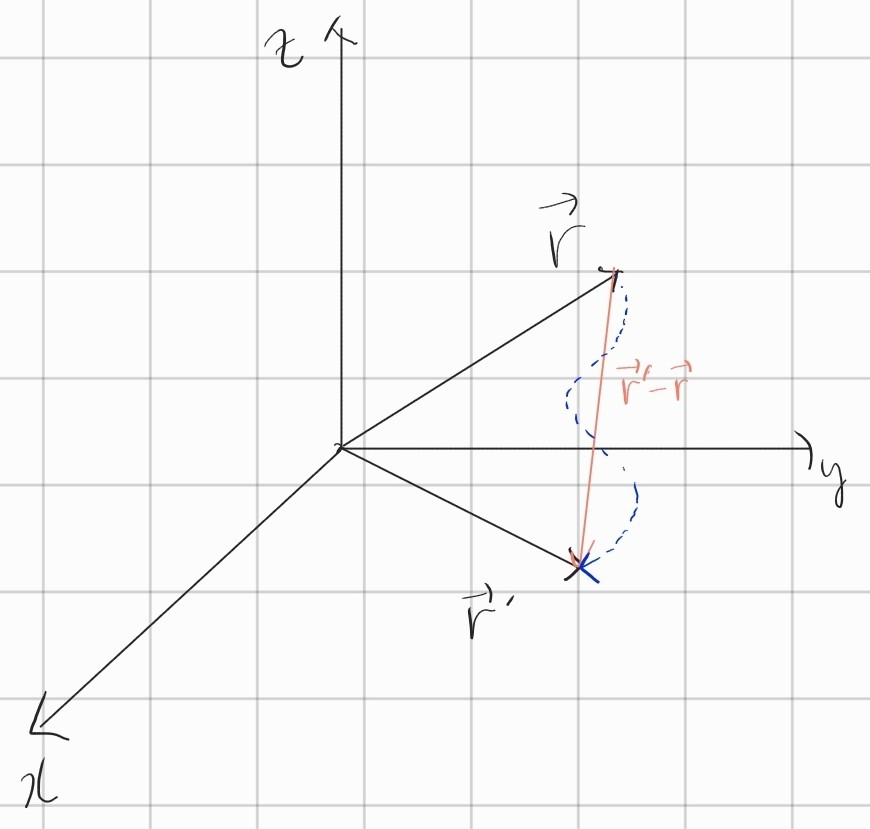
저 파란색 경로가 실제 이동 경로였다면 물체의 순간적인 움직임을 평균속도가 설명하진 못하겠죠. 그래서 이동시간을 확!! 줄여서 거의 0에 수렴하게 해 봅시다. 그렇게 된다면 속도는
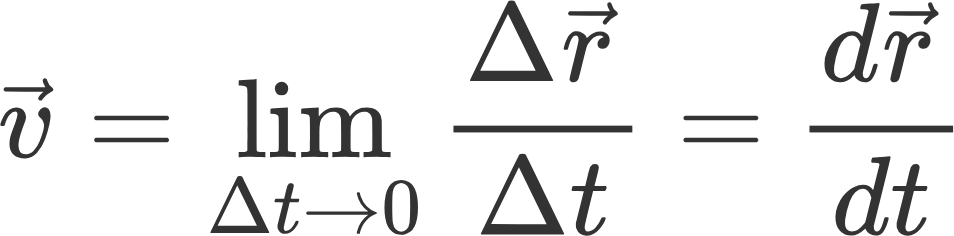
이렇게 정의되죠. dt는 매우 매우 작은 시간차를 의미하고 'dr벡터'는 dt동안의 변위를 의미합니다. 수학의 논리를 빌리면 '위치를 시간에 대해 미분'한 것이 '속도'가 되는 것이죠. 즉, 특정 '시각'에서의 '순간속도'를 함수로 나타낼 수 있는 것입니다. 이것을 그림으로 나타내면
이렇게 됩니다. 위치 곡선의 '접선의 기울기'가 속도가 되는 것이죠. 여기까지 어렵지 않나요? 여기서 중요한 것은 '속도'도 크기와 방향을 가진 '벡터'라는 점입니다. 그리고 이 '속도'의 절댓값이 바로 '속력'입니다.
느낌이 오나요? '인생은 속도가 아닌 방향'이라는 말이 틀린 이유는 속도에 방향이 포함되기 때문입니다... 물론 일상생활에서는 딱히 큰 구분을 하진 않죠..
여기까지 변위와 속도의 개념을 알아보았습니다. 재밌으셨나요? 다음 글은 이 개념의 수학적인 부분의 이해를 돕기 위해 함수를 조금 다뤄보도록 하겠습니다... 그렇게 어렵지 않을 거예요! 그럼 오늘도 좋은 하루 보내세요!
'고전역학' 카테고리의 다른 글
| 세상은 수학으로 움직인다?: 운동방정식 (0) | 2024.01.08 |
|---|---|
| 사과나무의 진실: 뉴턴의 운동법칙 (1) | 2024.01.03 |
| 아는 것이 힘? 이다: 힘 (0) | 2024.01.02 |
| 인생은 속도가 아닌 방향?: 변위와 속도 (2) (1) | 2024.01.01 |
| 자연을 구성하는 요소 (2) | 2023.12.27 |



