모두들 새해 복 많이 받으세요! 새해가 밝은 만큼 앞으로 하시는 일 다 잘되시길 바라겠습니다!
그리고 제 블로그도 많이 방문해 주시면 감사하겠습니다!
우리는 저번 글에서 변위와 속도의 개념에 대해서 알아보았습니다. 이번에는 이 개념의 수학적 이해를 돕기 위해서 위치와 속도에 관한 함수를 다뤄보며 설명을 해보겠습니다. 그렇게 어렵지 않으니 차근차근 살펴봅시다!
그전에 '벡터'와 '위치벡터'에 대해 모르시는 분들은 아래 링크를 한번 보고 와주세요!
https://wgco-physicspark.tistory.com/4('벡터와 스칼라' 편)
https://wgco-physicspark.tistory.com/5('위치벡터와 기저벡터' 편)


먼저 '시간에 따른 위치'를 나타내는 함수를

라고 하겠습니다. 여기서 변수 t는 '시간'을 의미합니다. 변위는 t1, t2가 정해졌을 때 어떤 시각 t1에서 t2까지의 '위치의 변화량'이 되겠죠. 식으로 나타내면

이렇게 나타낼 수 있습니다. 그리고 이 '위치'를 시간에 대해 미분한 것이 속도,
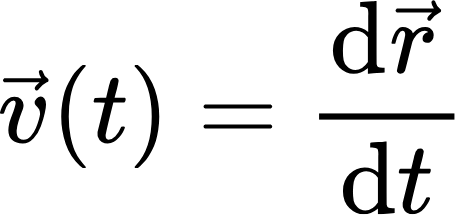
와 같이 표현되는 것이죠. 어떤 물체가 1차원 x축 상에서만 움직인다고 가정을 해봅시다. 그리고 시간에 따른 위치가

로 나타난다고 한다면 속도는
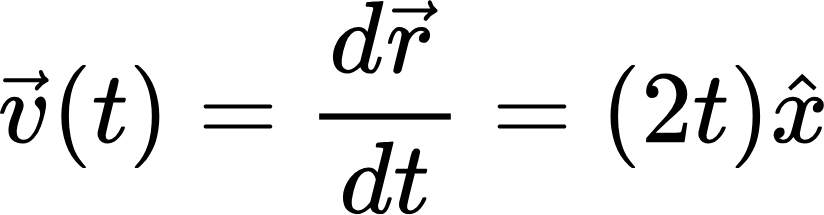
가 됩니다. 여기까지 어렵지 않으시죠? 그렇다면 이제 공간의 차원을 조금 더 확장시켜보도록 합시다.
만약 물체가 2차원 평면을 움직인다면 어떻게 될까요?

위치는 이렇게 나타나고 속도는
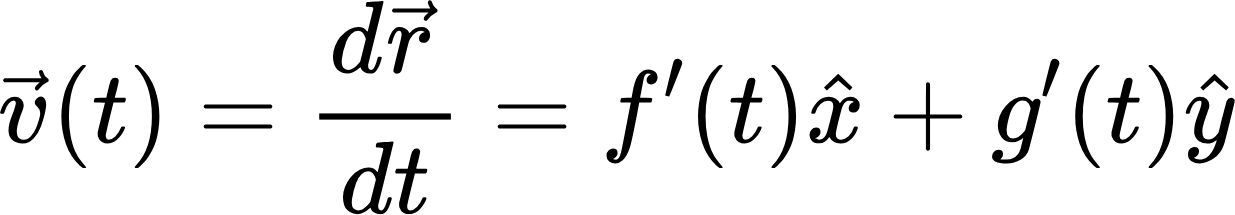
가 되겠죠. 감 잡으셨나요 그렇다면 3차원 공간에서 위치와 속도는

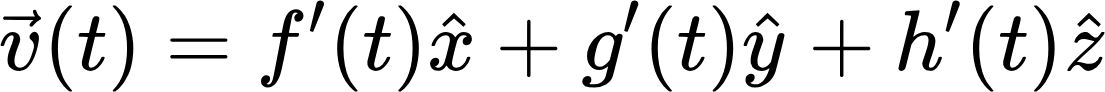
가 됩니다. 그래서 위치, 속도는 모두 벡터이기 때문에 각각의 축 방향을 가진 벡터들로 '분해'해서 따로따로 계산하는 것이 가능합니다. 그리고 단위벡터에 곱해져 있는 함숫값이 시간에 따라 양수, 음수 다 가질 수 있죠.
위치를 미분한 것이 속도면 반대로 속도 함수를 적분한 것은 위치함수가 되겠죠. 그리고 속도 함수의 t1에서부터 t2까지의 '정적분'값은 위치의 변화량, 즉 변위가 됩니다.

여기까지의 관계가 이해가 되실까요? 다음으로 '속력'은
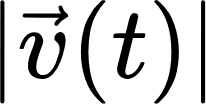
이렇게 속도의 절댓값으로 나타납니다. 즉, 이 속도 벡터의 크기를 나타내죠. 여기서 속도 벡터의 크기를 구해보면

가 바로 속력의 값이 되는 것입니다(벡터의 크기를 구하는 것은 위치벡터 편에서 확인하실 수 있습니다). 그래서 속력은 양수 값을 가질 수 밖에 없겠죠.
자, 이제 '가속도'라는 개념 하나를 더 소개해보도록 하겠습니다. 가속도는 '속도'가 얼마나 변하는가를 보는 것입니다. 그래서 '속도'를 미분한 것이 바로 '가속도가 되는 것입니다. 위치와 속도의 수학적 관계를 생각하면 이해가 쉬울 겁니다.

가속도 a벡터도 벡터이기 때문에 속도가 가지는 벡터로서의 특징을 다 가집니다. 이 가속도라는 아이는 '힘'과 관련하여 중요하게 등장하니 잘 봐두시기 바랍니다.
여기까지 우리는 변위, 속도, 속력, 가속도 개념을 수학적으로 알아봤습니다. 조금 어려우셨나요? 모든 물리 분야의 기초이기 때문에 지금 잘 이해하는 것이 중요합니다. 그럼 오늘도 좋은 하루 보내세요!
'고전역학' 카테고리의 다른 글
| [고전역학] 세상은 수학으로 움직인다?: 운동방정식 (0) | 2024.01.08 |
|---|---|
| [고전역학] 사과나무의 진실: 뉴턴의 운동법칙 (1) | 2024.01.03 |
| [고전역학] 아는 것이 힘? 이다: 힘 (0) | 2024.01.02 |
| [고전역학] 인생은 속도가 아닌 방향?: 변위와 속도 (1) (2) | 2023.12.31 |
| [고전역학] 자연을 구성하는 요소 (2) | 2023.12.27 |



