여러분은 지렛대의 원리에 대해서 많이 들어보셨을 겁니다. 힘점과 받침점 사이의 거리는 길고 받침점과 작용점 사이의 거리는 짧을수록 적은 힘으로도 큰 힘의 효율을 볼 수 있습니다. 왜일까요?

바로바로 돌림힘 때문입니다! 돌림힘(torque), 토크는 우리 생활에서 아주아주아주 많이 쓰이는 만큼 아주 중요한 개념입니다. 오늘은 이 돌림힘에 관해서 이야기를 나눠보겠습니다.

돌림힘의 정의는 다음과 같습니다.
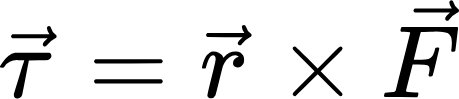
돌림힘, 즉 토크는 '질점의 위치벡터'와 위치벡터의 끝점에서 작용하는 '힘'의 외적입니다. 여기서 위치벡터의 시점은 질점의 회전축입니다. 이를 그림으로 나타내면

이렇게 되는 것이죠. 아직 외적에 대해서 모르신다면 (https://wgco-physicspark.tistory.com/10 '내적과 외적'편) 여기 링크로 들어가주시기 바랍니다!
돌림힘은 그림에서처럼 하나의 독립된 질점에 대해서 발생할 수도 있지만 독립된 질점이 아닌 연속적인 물체에 대해서도 당연히 발생을 합니다.

이런 원판(disk)에서는 원판의 어디에서든 회전축을 중심으로 돌림힘이 발생을 합니다.
다음으로 힘의 평형에 관해서 잠깐 이야기하도록 하겠습니다.
어떤 물체가 평형 상태를 이루기 위해서는 알짜힘(net force)가 0임과 동시에 알짜 돌림힘(net torque)도 0이어야 합니다.
예를 들어,

이렇게 양쪽에서 힘을 받고 있는, '밀도가 일정한' 막대기가 있다고 합시다. 이 막대기는 알짜힘과 돌림힘이 둘 다 0입니다. 일단, 보시다시피 크기가 같고 방향이 반대인 힘이 작용하기 때문에 알짜힘이 0입니다. 그리고 질량 중심이라는 회전축을 시점으로 위치벡터를 선정한 다음 양 끝점에서 돌림힘을 구하면 0이기 때문이죠.
하지만 만약 한 쪽의 힘이 질량 중심과 가까운 지점에 있었다면, 한 쪽의 위치벡터 크기가 달라져서 돌림힘 평형은 깨졌을 것입니다. 그래도 알짜힘은 여전히 0이겠죠.
그래서! 돌림힘 평형이나 돌림힘을 알기 위해서는 물체의 '질량중심'을 구하는 것이 중요합니다. 이는 다음에 다루도록 하겠습니다.
돌림힘은 다음 글에서 설명할 원운동과 밀접한 연관이 있습니다. 그래서 지금 잘 봐두셨으면 좋겠습니다.
그럼 좋은 하루 보내세요!
'고전역학' 카테고리의 다른 글
| 원운동도 가속운동이다: 구심력 (0) | 2024.01.29 |
|---|---|
| 인생은 회전목마와 같다: 원운동(circular motion) (0) | 2024.01.17 |
| 덜 아프게 맞는 법: 운동량과 충격량 (2) | 2024.01.14 |
| 세상은 수학으로 움직인다?: 운동방정식 (0) | 2024.01.08 |
| 사과나무의 진실: 뉴턴의 운동법칙 (1) | 2024.01.03 |



