안녕하세요! 오늘은 저번 글에 이어서 행렬의 기본 행 연산(elementary row operation)에 대해서 알아보도록 하겠습니다.
'기본 행 연산'은 행렬의 생김새를 바꾸어서 행렬식을 편하게 구하도록 하거나 연립방정식을 풀기 위한 것입니다. 이 연산에는 3가지 규칙이 있습니다.
1. i행과 j행을 맞바꾼다.
2. i행에 0이 아닌 상수를 곱해서 j행에 더한다.
3. i행에 0이 아닌 상수 k를 곱한다.
이 연산법칙이 중요한 이유는 크기가 큰 연립방정식을 구할 때 계산을 조금 더 편하게 할 수 있습니다. 또는, 기본 행 연산을 통해서 행렬을 '대각행렬'과 비슷하게 만들거나 한 '행'이나 '열'에 0을 많이 만들면 행렬식을 구하는 것이 훨씬 수월해질 것입니다.
이제 기본 행 연산을 사용해서 연립방정식을 풀어보도록 하겠습니다.
여기 연립방정식이 하나 있습니다.
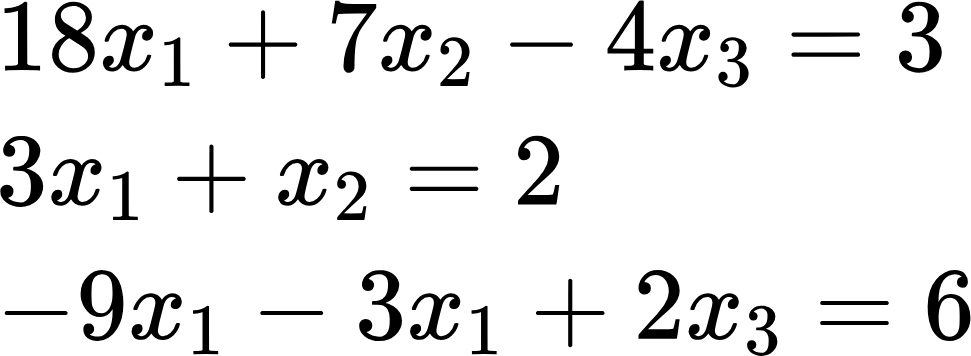
이 연립방정식을 변수 앞에 계수를 따서

이렇게 고칩니다. 그 다음 기본 행 연산을 두 행렬식에 동시에 적용하는 것입니다.
1. 3행에 2를 곱하고 1행에 더합니다.

2. 2행에 3을 곱하고 3행에 더합니다.

3. 1행과 2행을 교체합니다.

4. 2행에서 -1을 곱하고 1행에 더합니다.

5. 1행은 1/3을 곱하고 3행은 1/2를 곱합니다.

이렇게 왼쪽에 있던 행렬을 단위행렬로 바꾸면 왼쪽에 있는 행렬의 요소가 위에서부터 차례대로 x1,x2, x3가 되는 것입니다!
이 원리 자체는 '가우스 소거법'이라는 방식입니다. 기본 행 연산을 하는 방식 그대로 원래의 식을 조작하면서 따라가면 이 원리가 바로 이해가 될 것입니다. 그리고 기본 행 연산을 활용하여 행렬식도 더 간단하게 구해볼 수 있습니다.

이런 식으로 말이죠.
여기까지 기본 행 연산과 그 활용에 대해서 알아보았습니다. 다음에은 기본 행 연산을 이용하여 역행렬을 구하는 방식에 대해서 이야기해보겠습니다.
그럼 오늘도 좋은 하루 보내세요!